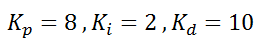Problema al implementar un programa asíncrono en VHDL

Supongamos que tenemos un programa muy simple en VHDL en el que prendemos y apagamos dos leds mediante dos interruptores: 

library ieee;
use ieee.std_logic_1164.all;

entity leds is
port( a,b : in std_logic;
     s1,s2: out std_logic);   
end leds;

architecture control of leds is
begin

s1 <= a;
s2 <= b;

end control;

Para la tarjeta de desarrollo Basys2 nuestro archivo .ucf quedaría:

# Interruptores
NET "a" LOC = P11;
NET "b" LOC = L3;

# Leds
NET "s1" LOC = M5;
NET "s2" LOC = M11;

Hasta aquí todo parece en orden e incluso nuestro programa funciona bien en la simulación. Pero un problema muy común entre los estudiantes de los primeros cursos de sistemas digitales es que al momento de cargar el archivo .bit de un programa asíncrono como este a una tarjeta de desarrollo, ésta se queda sin hacer nada. Esto ocurre porque la tarjeta espera arrancar por default con el oscilador interno aunque no lo usemos en el programa (razón por la que este problema muy rara vez se presenta en programas que si lo usan). Este problema se resuelve simplemente haciendo click derecho sobre "Generate Program File", buscar "Process Properties" que nos abrirá la siguiente ventana en la debemos buscar la categoría "Startup Options" y cambiar la opción de FPGA Start-Up Clock de CCLK a JTAG Clock:

Control PID para el modelo simple de una masa móvil

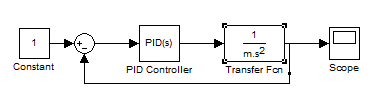
Supongamos que tenemos un pequeño vehículo de masa 'm' que se encuentra en una posición inicial x0 que queremos llevar hasta una posición final xr. Para simplificar las cosas supondremos que no existe fricción entre las ruedas y el suelo ni resistencia al aire. El modelo de nuestra planta queda descrito entonces por la 2da Ley de Newton:

dónde la fuerza F(t) es la entrada y la posición x(t) nuestra salida de la planta. Obteniendo la transformada de Laplace,su función de transferencia nos queda:

Observe que cuando a 'm' se le asigna una masa unitaria G(s) se convierte en un doble integrador. Para este modelo, como debe haberse tratado en cualquier curso de control, un controlador proporcional resulta ineficaz. Un controlador de este tipo únicamente mantendría oscilando el carrito al rededor de la posición deseada sin alcanzar nunca la estabilidad. Incluso considerando la resistencia al aire, este tipo de controlador mostrará una respuesta transitoria indeseable. Para control ideal, donde el carrito acelere y desacelere suavemente hasta detenerse justo (casi en este caso sin fricción ni resistencia al aire) en la posición que queremos requerimos un controlador PID. Las ganancias para controlar un doble integrador ideal son:

Corriendo nuestro modelo en Simulink estos son son los resultados: