Conversión Digital-Analógica por PWM filtrado en PIC16F15313

 Este apunte público tratará muchos conceptos y haré referencias a información extra para mantenerlo corto. Comenzaré con la razón por la que necesité hacer este programa. Requería construir un pulso para caracterizar un sistema (identificación de sistemas) a partir de su la respuesta. Un impulso o Delta de Dirac es una distribución que tiene la peculiaridad de tener un espectro que abarca todas las frecuencias. En teoría, si queremos saber cual será la respuesta de un sistema a todas las frecuencias entonces debemos aplicar como entrada una señal impulsiva. En la práctica hay algunos problemas. Es imposible construir un impulso ideal y a demás los sistemas físicos como los sensores están siempre limitados a una banda de frecuencias. Peor aún, al digitalizar la señal de un sensor analógico se restringe a un más el ancho de banda útil. Es por eso que en algunos casos en mejor utilizar una función Sinc (o seno cardinal) como entrada de caracterización ya que permite definir bastante bien el ancho de banda de trabajo. En mi caso particular, necesito una señal Sinc con un periodo de lóbulo principal de 1/(3.8kHz) o 263.16 us y con los bordes suavizados por una gaussiana. El periodo del lóbulo principal se mide entre sus cruces por 0. Su gráfica en el tiempo y su espectro se muestra a continuación:

 Se puede notar que he establecido mi ancho de banda de trabajo de 0 a 3.8kHz. Ahora lo que procede es escribir un programa en un microcontrolador que me de un PWM que codifique mi señal Sinc. Por restricciones de espacio, mi aplicación requiere de un microcontrolador muy pequeño por lo que elegí el PIC16F15313 que tiene solo 8 pines. Justo los que requería. En México pueden comprarlos en AG Electrónica. El circuito usado es el siguiente:

 

 

El código para el micro (en XC8) lo pueden encontrar bien comentado en este repo en mi Github. Por último, se diseñó un filtro pasa-bajas de orden 4 utilizando el programa Filter-Pro de Texas Instruments (al parecer ya no se puede descargar pero existe como aplicación web). Se eligió una frecuencia de corte de 12 kHz para tener un buen margen de operación y buena calidad de señal:

 Estoy usando el integrado MCP602 que tiene dos opams por integrado porque son los que tenía a la mano pero pueden utilizar un solo MCP604 que tienen 4 opamps por integrado (pueden comprar ambos en AG). El resultado de la implementación en físico se muestra en la siguiente captura de osciloscopio:

Optimización en Python con SciPy

Resolver problemas de optimización es una herramienta esencial para la ingeniería y la ciencia y debería ser una prioridad en los programas académicos. La bibliografía para aprender la teoría que podría sugerir es el capítulo 7 del libro gratuito Mathematics for Machine Learning. Por ahora me concentraré a detallar una nota para usar la función minimize() del modulo SciPy. Me estoy basando en gran parte en el ejemplo de APmonitor. No sólo será un traducción sino que añadiré detalles importantes que fueron omitidos en su tutorial.

En la jerga de optimización, se le llama función objetivo a la función que se desea optimizar alguno o algunos de sus argumentos. En este ejemplo la función objetivo a minimizar será:

La solución del problema de minimización consiste en encontrar los valores del vector x para los cuales la salida de la función objetivo sea mínima. En la práctica la función objetivo está sujeta a restricciones por lo que este ejemplo no será la excepción:

Restricción 1. El producto de todas las variables debe ser mayor o igual a 25.

Restricción 2. La suma de los cuadrados de las variables debe ser igual a 40.

Finalmente hay que considerar los intervalos que acotan a cada una de las variables:  

Para escribir el programa de Python usando el submódulo optimize de SciPy necesitamos saber lo siguiente. La función minimize() tomará, para este ejemplo, estos argumentos:

func. Una función que debe definirse con un único argumento vectorial y retornando un único escalar.
method. La lista de métodos de minimización disponibles aparecen en la documentación. Es importante saber que los únicos métodos que permiten optimización con restricciones son ''COBYLA", "SLSQP" y "trust-constr".
bounds. Lista de tuplas con las cotas para cada variable.
constraints. Lista de diccionarios donde cada uno tiene la esctructura:

• 'type': Tipo de restricción. 'eq' para igualdad o 'ineq' para desigualdad
• 'func': Nombre de la función que describe la desigualdad (debe crearse) 

Código completo:

Flor del Edén

Flor del Edén

En teoría de autómatas celulares, un "Jardín del Edén" es una configuración a la que no se puede llegar sin importar la condición inicial ni cuanto evolucione el programa que implementa al autómata. Pero un Jardín del Edén si puede ser una condición inicial del programa, de ahí las dos interpretaciones que le dieron el nombre: la de John Tukey que dice que sólo el creador de la simulación puede construirlo y otra que dice que "una vez perdido, no puede recuperarse". Este concepto ha generado experimentos filosóficos curiosos. En principio, si viviéramos en una simulación, bastaría encontrar un Jardín del Edén como marca de agua de los arquitectos de la Matrix para verificarlo. Esta idea es explorada en la novela de ciencia ficción "Ciudad Permutación" de Greg Egan. La Flor del Edén es un JdE del Juego de la Vida (GoL, The Game of Life ). Sé que John Conway odiaba ser famoso por The Game of Life, pero este post era la mejor referencia que podía hacer en su memoria.

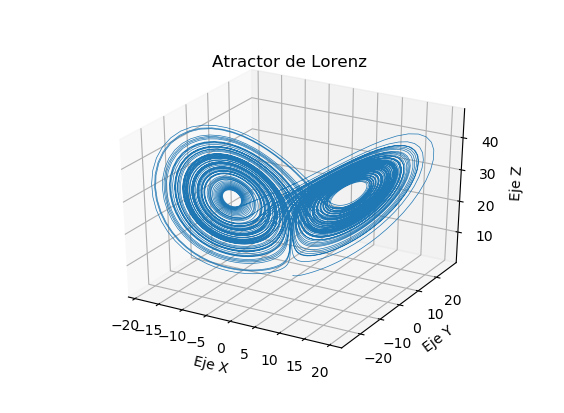
Atractor de Lorenz en Python usando odeint()

Este programa es un ejemplo de dos temas interesantes: el atractor de Lorenz y la resolución de un sistema de ecuaciones diferenciales ordinarias usando el modulo scipy. El sistema que resolveremos (el sistema de Lorenz) consta de 3 ecuaciones diferenciales acopladas (que funcionan de manera interdependiente). Nótese que he cambiado la notación que aparece en el articulo de Wikipedia a una forma vectorial:

Esta notación facilita el entendimiento de la sintaxis de la función  odeint(). Lo primero que debe hacerse, después de importar los módulos correspondientes, es contruir una función que tome como argumentos el vector u y t y retorne el vector de derivadas de u. En este caso particular las ecuaciones diferenciales no dependen de t (son autónomas), aún así es necesario poner como argumento a t porque lo exige la sintaxis de la función odeint(). Después se establece una condición inicial para el vector u y se construye una lista de valores para t sobre el intervalo en que nos interese tener a la solución. Finalmente se coloca todo lo anterior como argumentos del solver odint() como aparece en el código completo:

Esta será la gráfica resultante (El Atractor Extraño de Lorenz):

Generar imagenes PNG de ecuaciones en LaTeX

El archivo que pueden usar como plantilla es el siguiente:

Para poder generar el PNG deben colocar --shell-escape como opciones para el compilador. En Texmaker/TeXstudio pueden hacerlo yendo a Opciones->Configurar Texmaker/TeXstudio:

Yo utilicé esta función para hacer en Gimp stickers matemáticos impresos en papel couché adhesivo:

Nota: Si usas Windows es un poco más complicado: LaTeX to PNG on Windows.

¿Existe un método universal para resolver problemas?

No tengo duda de que los genios no nacen, sino se hacen a través de practica efectiva acumulada (recomiendo ver estos videos [Pt1,Pt2]). Entiendo también que debe haber una componente genética en el proceso, pero no la considero sustancial. Si todos podemos ser genios, entonces la pregunta ahora es si existe un método efectivo que no vuelva maestros de la resolución de problemas. No podría dar alguno pero si creo que si es posible hacer un bosquejo inicial que nos lleve al método que buscamos si lo refinamos lo suficiente.

Definir el problema. Aparentemente esto no parece llevarnos a algún lado pero pensémoslo de otra manera. Cuando comencé a aprender Prolog me pareció muy interesante el hecho de que la solución a un problema se encuentra únicamente a través de la definición correcta del problema. No es que la solución brote de la anda. Prolog al ser un lenguaje declarativo, su interprete utiliza una serie de algoritmos que procesan los "hechos" del problema. Si le das al interprete una descripción de los hechos lógicamente consiste al problema que quieres resolver entonces tendrás su solución. Esto es un ejemplo de como un replanteamiento del problema puede abrirnos un camino a su solución.

Dividir el problema en sub-problemas. Si el problema es simple (no necesariamente fácil de resolver, pero simple en el sentido de no ser divisible) este paso no será necesario. Pero si el problema es complejo, resulta muy útil partirlo en diferentes problemas (en principio más fáciles de resolver). Pudiera ser el caso que para resolver el problema sea necesario primero desarrollar alguna habilidad en particular o investigar sobre algún tema en especifico (la práctica e investigación también son sub-tareas en este sentido).

Cuestionar las restricciones. Este punto está relacionado con la definición del problema. Una vez que lo hemos definido tenemos que pensar: ¿son necesarias todas las restricciones que estoy considerando o estoy poniendo restricciones que no existen en el problema? Esto se conoce también como pensar fuera de la caja. Es necesario hacer notar que hace falta definir la caja antes de hablar sobre lo que está fuera de ella. Por ello, esto debe hacerse sólo después de hacer al menos un primer intento de definición del problema.

Explorar los recursos disponibles. Cuando se haya definido el problema y descartado restricciones ficticias es hora de poner manos a la obra. Se deben hacer las siguientes preguntas: ¿qué podría usar de todo lo que sé y de todo lo que está a mi alrededor (o en el ambiente o contexto del problema)? ¿he resuelto antes problemas similares?, en caso de que me falte experiencia o información ¿dónde podría conseguirla o a quién podría consultar? Una técnica también inspirada de Prolog es hacer un diccionario de hechos y reglas , es decir, anotar o tener presente en la mente todas las características de los elementos y relaciones de causa y efecto tanto en el problema como en el ambiente del problema [cosas como: "A es un T","si ocurre X entonces Y", "si se quita W entonces Z", etc].

Pensar al revés. Sé que quisiéramos que las soluciones a nuestros problemas estén a un sólo paso de nosotros. A veces es verdad y esa solución se hace evidente al definir el problema de forma ingeniosa o de eliminar restricciones ficticias. Pero muchas veces los problemas requieren de una solución de varias etapas. Una manera de atacar este tipo de problemas es partir del estado deseado (meta) que llamaremos "G(n)" y tratar de pensar: ¿cual tendría que ser el estado anterior inmediato G(n-1)? ¿cómo podría resolver de G(n-1) a G(n)? Este proceso es básicamente una división en subproblemas pero en orden temporal inverso hasta llegar al primer paso [G(1) a G(2)]. Esto se conoce como análisis retrospectivo.

Resistir la frustración. En lo personal creo que este el punto más importante de todos. No es un aspecto metodológico sino psicológico, pero que al dominarlo nos da una herramienta invaluable. No siempre veremos la solución al primer intento. Somos humanos y no puedo pedir no sentir enojo o desesperación ante una falla, pero si pido aguantarla. La buena noticia es que la resistencia o tolerancia a la frustración es como un musculo que se vuelve más fuerte entre más se ejercite. Algunos recomiendan tomar descansos entre las fallas. A mi en lo personal me ha servido muchas veces la actitud de "no me voy a ir de aquí hasta que funcione". Depende realmente de la persona, pero la idea es aguantarse y hacerse fuerte ante el fracaso.

Buscar tener nuevos problemas. Esto pareciera ser algo que todos queremos evitar, pero volverse un masoquista intelectual te da, con el tiempo, un repertorio muy amplio de experiencias que te permite resolver problemas similares, muchas veces con sólo recordar y modificar ligeramente soluciones pasadas.

Todo lo anterior es un apunte personal. No voy a decir que es el elixir sagrado de la resolución de problemas. Pero es lo que me ha funcionado y son notas que iré extendiendo o mejorando sobre la marcha de mi vida.

Diagramas de estado en LaTeX (TikZ)

TikZ es una paquetería muy poderosa que permite construir graficos complejos en LaTeX. En esta entrada sólo veremos como crear diagramas de estados para FSM's (Finite State Machine). Primero importamos el paquete y las librerías que vamos a utilizar:

\usepackage{tikz}
\usetikzlibrary{automata, positioning, arrows}

La creación de un diagrama se describe a continuación.

Estados

\node[state,opciones,posición] (nombre) {etiqueta de texto};

Las opciones para el tipo de estado contexto de las FSM son:

• initial : Estado inicial
• accepting: Estado de aceptación
• Vacío para un estado genérico 

 La posición puede establecerse de las siguientes maneras:

•  of= estado : right, left, above, below (o una combinación, ejem: above right ). Ejemplo:

\node[state, right of=q1] (q2) {$q_2$};

• xshift=x, yshift=y : Da control manual de la posición relativa a un estado. Ejemplo:

\node[state, right of=q1, xshift=1cm] (q2) {$q_2$};

• at (x,y) : Coloca la figura del estado en una posición especifica en la figura. Ejemplo:

\node[state] (q) at (2, 3) {$q$};

Flechas de transición

\draw (nodo origen) edge[opciones] node{etiqueta de flecha} (nodo destino);

• El nodo de origen debe llevar el nombre y no la etiqueta del estado.
• Las flechas por defecto rectas. Se pueden curvar con la opción bend left/right.
• Los loops se crean con la opción loop above/below/left/right. 

Ejemplo

Multiplicación en punto fijo Pt. 2 [formato fixdt(signed,n,s,b)]

Esta entrada es una continuación del tema de multiplicación punto fijo y tocará el tema de un formato de mapeo lineal que permite ajustar números enteros a un rango lineal arbitrario como puede ser los rangos de voltaje estándar para DAC's y ADC's. El formato es el siguiente:

fixdt(signed,n,s,b) 

• signed: toma el valor de 1 si el entero almacenado es signado y 0 en caso contrario.
• n:  longitud en bits del entero almacenado. 
• s: pendiente de la función de mapeo lineal. 
• b: bias de la función de mapeo lineal.

En esta convención un número con parte entera y decimal se representa de la siguiente manera:

 El rango de este formato queda definido por sus parámetros de la siguiente manera:

 La multiplicación queda definida cómo:

 La multiplicación es mas complicada que en el formato fixed(signed,n,l) pero se simplifica cuando b = 0 siendo en este caso similar a la multiplicación en el otro formato. El siguiente paso en definir el procedimiento para computar los valores de n, s y b según el intervalo continuo en que el que deseemos trabajar. Al igual que el formato anterior ,el parámetro n define los valores máximos para los enteres almacenados. Por tanto, teniendo definidos los límites del intervalo real y del intervalo entero, los valores de s y b se calculan resolviendo el siguiente sistema de ecuaciones:
 

 Realizaremos un ejemplo práctico para demostrar la utilizad de este formato su ventaja con respecto a fixed(signed,n,l). Implementaremos en un FPGA un generador de señal cosenoidal (he escrito una entrada sobre los detalles de estos generadores). Utilizaremos una DAC LTC1661 que tiene una resolución de 10 bits y un rango de salida de 0-Vreff*(1023/1024). Las salidas Vcc de la tarjeta que voy a utilizar son de 3.3 volts por lo que este intervalo será aproximadamente de 0-3.3 V. Ya que esta DAC no puede dar salidas de voltaje negativo el valor para signed sera '0'. Con esta información podemos encontrar los valores para establecer nuestro formato. Podemos obtenerlos mediante este código de Matlab:

minimo = 0; %Volts
maximo = 3.3; % Volts
is_signed = false;
word_length = 10;

[E_min, E_max] = range(fi([], is_signed, word_length, 0));

A = double ([E_min, 1; E_max, 1]);
b = double ([minimo; maximo]);
x = A\b;
format long g
slope = x(1)
bias = x(2)

La ejecución del código nos da una pendiente s = 0.0032258064516129 y un bias b = 0. La señal para este ejemplo tendrá una frecuencia de 0.05 Hz y un periodo de muestreo de 1 segundo (si pueden usar un osciloscopio pueden probar con una frecuencia más alta y un periodo de muestro más corto). Generaremos un código VHDL con HDL Coder a partir de este modelo de Simulink:

Los subsitemas que he llamado Fixed-Point Multiplication contienene la implementación de la multiplicación que hemos descrito aquí. Dado que b = 0 la multiplicación de punto fijo simplemente se define como el producto de los enteros almacenados y la pendiente s:

 Algo que podría resultar confuso y difícil de entender al principio es el por qué el producto con s se realiza en formato fixed(signed,n,l). La respuesta es que ese formato se utiliza para principalmente para la multiplicación de números fraccionales en un entorno que solo permita trabajar con números enteros de forma interna (que es el caso de nuestro sistema de hardware). El formato de mapeo lineal fixdt(signed,n,s,b) sólo se encarga de que las operaciones entre enteros tengan el sentido físico que esperamos de forma externa. Esto tambien explica un segundo hecho que tambien puede resultar confuso: las operaciones entre enteros se realizan en modo signed (para facilitar las restas) aunque se ha definido el modo unsigned. 

Para generar el código nos vamos a Code > HDL Code > Generate HDL. Para la comunicación SPI con la LTC1661 he modificado un código que había publicado anteriormente. Los módulos son los siguiente:

• Divisor
• DAC_SPI
• Generador_Coseno_HDL (Generado por HDL Coder) 

El esquemático del sistema es el siguiente:

Nota: durante la generación del código se indica que el reloj para el modulo del generador sea el doble del establecido. En este caso el divisor tiene una salida de 2 Hz.

Según la simulación, y si implementamos correctamente las cosas, las secuencia de voltaje que deberíamos ver experimentalmente a la salida del DAC es la siguiente:

Aquí muestro un video donde se puede ver que no tengo un buen multímetro y tuve que aumentar a 4 segundos el periodo de muestreo para dar tiempo de estabilizar las lecturas:
Referencias
Compute Slope and Bias, MathWorks
Fixed-Point: Rage and Precision, MathWorks 

Generación de una señal coseno discreta

Podemos generar una función senoidal o cosenoidal de forma discreta mediante una ecuación de diferencias que es obtenida a partir de la transformada Z de una función senoidal o cosenoidal según sea el caso. Esta ecuación de diferencias es fácilmente implementable en un microcontrolador o FPGA. En este ejemplo crearemos un generador de señal cosenoidal. Partimos de la transformada Z de una función coseno discreto considerándola como la respuesta al impulso de la función de transferencia de un sistema Y(z)/X(z):

Dónde W0 es la frecuencia angular en tiempo continuo y Ts es el tiempo de muestreo [ver mi entrada sobre el concepto de frecuencia en tiempo discreto]. Multiplicamos ahora por z^-2/z^-2 para obtener un modelo físicamente sintetizable (debido a que los valores positivos en los exponentes de z implican muestras desde el futuro):

Multiplicamos ambos lados por el denominador de la función de transferencia y despejamos para Y(z):

Aplicamos transformada Z inversa para obtener finalmente nuestra ecuación de diferencias:

Para simular el generador utilizaremos Xcos de Scilab que es una alternativa de código abierto de Simulink [si no están familiarizados con esta herramienta aquí hay un video curso en español]. Antes de colocar los bloques debemos ir a menú superior en Simulation>Set Context y definimos las siguientes variables:

Ts = 0.1
W0 = 2*%pi/10
k0 = cos(W0*Ts)
k1 = 2*k0
 
El diagrama en Xcos es el siguiente:

Recordemos que hemos supuesto desde el principio que x[n] = delta[n]. La función Delta de Kronecker (impulso discreto) es un super bloque formado por el siguiente subsistema:

Dónde el retardo 1/z está inicializado a 1. Obsérvese que en el diagrama principal estamos enviando los resultados de la simulación al workspace. Personalmente, las gráficas nativas Scilab me parecen feas. Para hacer una grafica en Python exportaremos los datos de la simulación a un archivo CSV con el siguiente comando en la consola de Scilab después de ejecutar la simulación:

csvWrite([A.time,A.values],'cos_data.csv',',')

Teniendo el archivo podemos generar una gráfica en Python con el siguiente código:

import numpy as np
import matplotlib.pyplot as plt

A = np.loadtxt('cos_data.csv',delimiter = ',')

plt.stem(A[:,0],A[:,1])
plt.ylim([-1.5,1.5])
plt.grid(True)
plt.xlabel('Ts*n')
plt.ylabel('y[n]')
plt.show()

  Se deja como ejercicio construir un generador para función seno.

Multiplicación en punto fijo [formato fixdt(signed,n,l)]

Aunque al principio pueda chocar con la intuición, es posible realizar de forma digital una multiplicación de dos números con parte entera y decimal utilizando únicamente números enteros. De hecho, para aplicaciones de instrumentación científica o simulaciones numéricas dónde la precisión sea la prioridad es incluso aconsejable evitar el uso del famoso punto flotante. Recomiendo enormemente ver este capítulo del canal PBS Infinite Series para entender desde el punto de vista matemático el problema fundamental de los tipos double y single. En pocas palabras este problema radica en la en las limitaciones en la accesibilidad sobre la recta numérica computable. La resolución del punto variable no es homogénea a lo largo de todo su rango. Una segunda limitación de las operaciones de punto flotante tiene que ver a su costo de implementación en hardware; construir circuitos digitales de punto flotante consumen más recursos en un FPGA.

El formato de punto fijo con el trabajaremos en esta entrada es:

 fixdt(signed,n,l)

• signed : toma el valor de 1 si el entero almacenado es signado y 0 en caso contrario
• n : longitud en bits del entero almacenado 
• l : longitud en bits de la parte fraccional

En esta convención un número con parte entera y decimal se representa de la siguiente manera:

Los parámetros n y signed nos da el rango del formato:

A partir de la relación entre el Valor del Mundo Real (como se le llama en la jerga de punto fijo y denotaremos como Val) y el entero almacenado (que denotaremos por E) podemos definir la multiplicación de punto fijo de la siguiente forma:

Esto significa que la multiplicación se realiza como el producto de dos enteros mas un bitshift a la derecha de l locaciones. Para comprender mejor este formato realizaremos un ejemplo práctico concreto. Supongamos que queremos digitalizar una señal de voltaje sinusoidal de amplitud de 2 V con una frecuencia de 1 Hz mediante un ADC de 12 bits de resolución y un rango de entrada de 0-4 V. Supongamos que una vez digitalizada la señal queremos realizar un escalamiento de 0.321 y enviar esta nueva señal a un DAC de la misma resolución y rango. ¿Cómo resolveríamos el problema sin utilizar operaciones de punto flotante?

Bien, usaremos el formato fixdt(signed,n,l) para este ejemplo. Lo primero que debemos hacer es establecer los parámetros del formato. Ya que nuestro ADC no puede leer voltajes negativos, el parámetro signed será igual a 0. Dado que la resolución es de 12 bits entonces n = 12. Sabiendo que el voltaje máximo de lectura es 4 V encontramos el valor l de la siguiente manera:

Tenemos que el valor de l es 10 dando un rango de 0-3.99 V. Entonces el formato para nuestro ejemplo queda definido así: fixdt(0,12,10). El siguiente paso en convertir la ganancia de 0.321 en formato fixdt(0,12,10):

El equivalente de la ganancia resulta ser: 329. Podemos realizar ahora una simulación de nuestro ejemplo en Simulink y comparar el desempeño de la operación de punto fijo contra la de punto flotante:

Click para agrandar

El opam en el circuito añade el offset necesario para levantar la señal de la fuente y pueda ser adquirida por el ADC. Los bloques de ADC y DAC son simplemente subsistemas que realizan las operaciones de conversión de decimal a fixdt(1,12,10) y de muestro ZOH. Si bien Matlab/Simulink permite realizar las conversiones al formato fixdt(signed,n,l), decidí manejar uint16 para poder generalizar el ejemplo para ser implementado en microcontroladores y no sólo en FPGA's. Nuestro formato fixdt(0,12,10) cabe en un uint16 y eso también permite hacer una intuición más clara de que simplemente trabajamos con formatos enteros convencionales. La gráfica resultante con la comparativa es la siguiente:

Vemos que la correspondencia entre las operaciones de punto fijo y punto flotante son muy buenas. Podemos ahora a aventurarnos a escribir un codigo VHDL para nuestra operación de escalamiento de este ejemplo:

La simulación del módulo mostrando algunos valores de ejemplo para los enteros almacenados de entrada y salida es la siguiente:

 Click para agrandar

Para finalizar quisiera hacer un último comentario. Quizá notaron que tuvimos mucha suerte al calcular el valor del exponente l y nos dio un número que se ajustaba perfectamente al rango del ADC. No fue suerte, yo elegí el rango para que este ejemplo fuera más sencillo. En la practica los DAC's suelen tener rangos de 0-5.2 V o 0-3.3 V. ¿Que se hace en esos casos? Aquí es donde entra un nuevo formato: fixdt(signed,n,s,b). Pero hablaremos de él en otra entrada.

Referencias:

Fixed-Point: Rage and Precision, MathWorks 

Instalación de GNU Scientific Library (Debian)

GNU Scientific Library (GSL) es una librería numérica para C/C++, al parecer, poco conocida fuera del ámbito académico especializado. Tiene un repertorio de rutinas comparable con el popular módulo SciPy para Python. Encuentro muy útil GSL para sistemas con Linux embebido en robótica o IoT, especialmente en aplicaciones que requieran la operación de estos sistemas de tiempo real. Recomendaría echarle un vistazo si trabajan en proyectos serios con Raspberry Pi's o UDO's que requieran cálculos numéricos avanzados. Su documentación está bien estructurada y es muy amigable. El único inconveniente es que no hay muchos ejemplos y ayuda ahí afuera (ni siquiera en Stack Overflow) así que habrá que leer cuidadosamente el manual de referencia.

Para instalar GSL en Debian y derivados:

sudo apt-get install libgsl0ldbl libgsl0-dev 

Probaremos la instalación con el siguiente ejemplo con operaciones de números complejos (revisar documentación):

#include <stdio.h>
#include <gsl/gsl_complex.h>
#include <gsl/gsl_complex_math.h>

int main (void){
 
  //Declaración de variables complejas
  gsl_complex z,w,u;
 
  //Asignación de valores
  GSL_SET_COMPLEX(&z,3,4);  //z = 3+4i
  GSL_SET_COMPLEX(&w,4,5);  //w = 4+5i

  //ejemplos de operaciones
  u = gsl_complex_add(z,w);
  printf("z + w = %2.f + i%.2f\n",u.dat[0],u.dat[1]);
  u = gsl_complex_mul(z,w);
  printf("z*w = %.2f + i%.2f\n",u.dat[0],u.dat[1]);
  u = gsl_complex_log(z);
  printf("log(z) = %.2f + i%.2f\n",u.dat[0],u.dat[1]);
  u = gsl_complex_exp(gsl_complex_add(z,w));
  printf("exp(z+w) = %.2f + i%.2f\n",u.dat[0],u.dat[1]);
  return 0;
}

Compilamos y ejecutamos desde terminal con:

gcc GSL_Complex_demo.c -lgsl -lgslcblas ; ./a.out

Experimentando con autómatas celulares

Encontré por accidente el libro The New Kind of Science de Stephen Wolfram mientras buscaba libros de estadística en la biblioteca de la FCFM de la BUAP. Después de leer los primeros capítulos no pude evitar probar en Python algunos autómatas celulares. Es increíble el como con reglas tan simples se puede generar tanta complejidad. Sólo observen, tomemos una una linea de n casillas de largo. Cada casilla puede contener un '1' o un '0'. Supongamos que inicialmente la linea contiene solo '0' exceptuando la casilla n/2 que inicializamos con '1'. Nuestro pequeño autómata se encargará de generar una nueva linea de n casillas debajo de la inicial rellenando las casillas de la nueva linea de acuerdo a una función booleana cuyas entradas son casillas de la linea anterior. El autómata tiene un tamaño de 3 casillas y va rellenado las casillas de la nueva linea moviéndose una casilla a la vez hasta terminar todo el array. Un ejemplo para un autómata sería:

 dónde las casillas blancas representan '0' y las negras '1'. Consideremos un autómata un poco más complicado definido por el siguiente conjunto de reglas:

 Podemos expresar la regla anterior como una función booleana de la siguiente forma:

la cual podemos reducir mediante factorización a la forma:

El código en Python para este autómata celular queda:

import numpy as np
import matplotlib.pyplot as plt

n = 500
iline = np.zeros(n)
iline[n/2] = 1;
lines= [iline]

def rule(A,B,C):
    X = A and not(C) or not(A) and C
    return X

for i in range(0,n):
    line = lines[i]
    nline = np.zeros(n)
    for j in range(0,n-2):
        if rule(line[j],line[j+1],line[j+2]) :
            nline[j+1] = 1
    lines.append(nline)
   
lines = np.array(lines)

plt.imshow(lines, cmap = 'gray')

Y el espectacular resultado graficado es:

La figura resultante es un fractal conocido como Triángulo de Sierpinski y el autómata que lo genera se conoce como Regla 90.

Entendiendo a las señales analíticas (muestras I/Q)

Las muestras I/Q son una representación matemática discreta de una señal de radiofrecuencia cuya característica más útil es tener un espectro de frecuencia negativa nulo (un espectro compacto y asimétrico). Dado que el procedimiento de obtención de estas muestras involucra una reducción de frecuencia, su uso esta muy extendido en en las aplicaciones de radio definido por software y comunicaciones digitales en general. Las dos características anteriores nos dan dos ventajas: la primera elimina la redundancia en el espectro y la segunda permite reducir en el ancho de banda.

¿Cómo se obtiene una representación compleja de una señal real? Para el caso continuo el proceso es el siguiente:

 Simplemente se multiplica a la señal de radiofrecuencia por un sinusoide complejo y se aplica un filtro pasa-bajas para eliminar la redundancia en el espectro. Esto es lo que se conoce como señal analítica. Este procedimiento se vuelve más claro en el dominio de la frecuencia:

Recordemos que una multiplicación en el dominio del tiempo se manifiesta como una convolución en el dominio de la frecuencia. La convolución entre el espectro asimétrico de un sinuosoide complejo produce un corrimiento en frecuencia, el cual está dado por la frecuencia del sinusoide complejo (que lleva la etiqueta de LO por Local Oscillator) .

Ahora bien, el proceso anterior es puramente matemático. ¿Cómo se hace en el mundo real? El problema se resuelve implementando un modulador en cuadratura como se muestra en el siguiente diagrama:

 Tomando en cuenta a la identidad de Euler, una multiplicación por un sinusoide complejo se emula como la multiplicación y filtrado separado de dos sinusoides reales en cuadratura (heterodino en cuadratura). Posteriormente, al digitalizar independientemente a cada una de las componentes, se consideran a las muestras del ADC en cuadratura como la parte imaginaria multiplica por -1. La I viene de In-phase y la Q de Quadrature. Prácticamente todos los dongles SDR que pueden conseguirse fácilmente en el mercado como los RTL's y el FunCube funcionan de esta manera. En la siguiente entrada haremos un ejemplo con GNU Radio para clarificar aún más las cosas.

Referencias:
"RTL-SDR: Inexpensive Software Defined Radio", EE123 University of California Berkeley
"I/Q Data for Dummies", Mikael Q Kuisma
"Complex Sinusoids", PDS Related

Concepto de frecuecia en tiempo discreto

Este es un tema que si no se entiende bien al principio de un curso de procesamiento digital de señales puede acarrear muchos problemas al ir avanzando en temas más complicados. En esta entrada trataré de explicar lo más claro posible lo que es la frecuencia de una señal discreta. Primero, comencemos describiendo a una función cosenoidal en tiempo continuo con la notación del Proakis [1]:

El subindice a se utiliza para denotar que x_a(t) es una señal analógica y no confundirla con su contraparte discreta x[n]. Ahora, tomemos esta misma señal discreta y multipliquémosla por tren de pulsos unitarios con un periodo de muestreo Ts (proceso conocido como muestreo).  Gráficamente, el resulto obtenido es el siguiente:

Tenemos ahora una nueva función que depende de una variable entera n multiplicada por el periodo de muestreo Ts. Es este escalamiento por Ts lo que permite que la señal discreta x[n] coincida en el tiempo con la señal x_a(t). x[n] es una nueva señal que está definida en función de una secuencia de números enteros que representan una posición en un arreglo de datos (estas posiciones pueden tomar valores negativos si se toman con respecto a un origen arbitrario en el arreglo):

Como consecuencia del teorema de muestreo de Nyquist-Shannon, sólo es posible obtener información sobre una señal o componente a una frecuencia dada sin riesgo de ambigüedades (conflictos con sus alias) mientras su frecuencia sea menor o igual a la mitad de la frecuencia de muestreo (que es simplemente el inverso de su periodo de muestreo Fs = 1/Ts). Por lo tanto, la frecuencia relativa (también llamada frecuencia normalizada) esta limitada al intervalo:

Si se grafica un ejemplo numérico, resulta bastante intuitivo visualizar que cuando un coseno discreto tiene una frecuencia relativa de pi radianes por muestra se alcanza el periodo mínimo distinguible para una función periódica discreta. Los sinusoides en tiempo discreto muestran periodicidad en frecuencia. Esto significa que los sinusoides discretos que guarden una diferencia en frecuencia de 2*pi son idénticos. Esto puede verse más claramente en esta animación que hice en Matlab:

Naturalmente, lo que nos interesan son los parámetros físicos a los que las señales en tiempo discreto hacen referencia. El periodo de muestreo Ts es el puente clave para darle significado en tiempo continuo a estas señales. Resumiendo las transformaciones de frecuencia:

 Referencias:
Sec. 1.3 "Concepto de frecuencia en señales continuas y discretas en el tiempo",  "Tratamiento Digital de Señales", John G. Proakis
Teorema del Muestreo, L. Javier Morales Mendoza, UGto