Atractor de Lorenz en Python usando odeint()

Este programa es un ejemplo de dos temas interesantes: el atractor de Lorenz y la resolución de un sistema de ecuaciones diferenciales ordinarias usando el modulo scipy. El sistema que resolveremos (el sistema de Lorenz) consta de 3 ecuaciones diferenciales acopladas (que funcionan de manera interdependiente). Nótese que he cambiado la notación que aparece en el articulo de Wikipedia a una forma vectorial:

Esta notación facilita el entendimiento de la sintaxis de la función  odeint(). Lo primero que debe hacerse, después de importar los módulos correspondientes, es contruir una función que tome como argumentos el vector u y t y retorne el vector de derivadas de u. En este caso particular las ecuaciones diferenciales no dependen de t (son autónomas), aún así es necesario poner como argumento a t porque lo exige la sintaxis de la función odeint(). Después se establece una condición inicial para el vector u y se construye una lista de valores para t sobre el intervalo en que nos interese tener a la solución. Finalmente se coloca todo lo anterior como argumentos del solver odint() como aparece en el código completo:

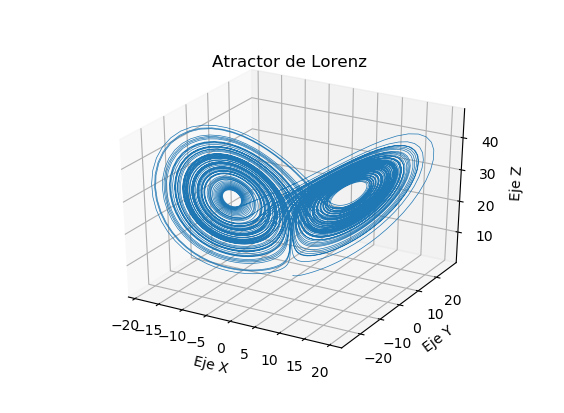
Esta será la gráfica resultante (El Atractor Extraño de Lorenz):