Simulación de circuitos eléctricos en Simulink

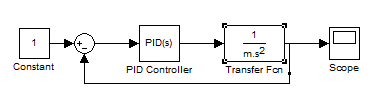
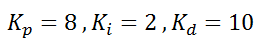Bloques usados:

Solver Configuration: (Simscape>Utilities)
Voltage Sensor: (Simscape >Foundations Library>Electrical>Electrical Sensors)
Current Sensor: (Simscape >Foundations Library>Electrical>Electrical Sensors)
PS-Simulink Converter: (Simscape >Utilities)
Resistor  (Simscape>Foundations Library>Electrical>Electrical Elements)
Electrical Reference  (Simscape>Foundations Library>Electrical>Electrical Elements)
AC Voltage Source     (Simscape>Foundations Library>Electrical>Electrical Sources)
Mux  (Simulink >Common Used Blocks)
Scope  (Simulink>Sinks)

Para este modelo se dejó la configuración del Solver en default con la fuente de voltaje a 10 V pico-pico a 60 Hz y la resistencia es de 50 ohms. El tiempo de simulación es de 0.06 segundos.

Nota: Cómo activar las leyendas en el Scope.

Guadalajara

Creo que siempre recordaré Guadalajara como el más agridulce de mis viajes. Tenía expectativas muy altas con la ciudad y con mis pretensiones, pero algo bajas con aquel congreso de astrobiología. Todo fue al revés. La ciudad, aunque bastante limpia y ordenada a mi parecer, no era precisamente la hermosa urbe colonial que tenía en la mente. Fue sin lugar a dudas uno de los mejores congresos a los que he asistido. Después de malas impresiones por ver una y otra vez en congresos anteriores trabajos mediocres hechos por estudiantes forzados, servicios sociales y gente que sólo va a alcoholizarse en la ciudades sede, no esperaba mucho. Cambié inmediatamente de opinión y me alegró saber que aún hay muchos estudiantes verdaderamente apasionados por la ciencia. Hice muy buena amistad con los compañeros de mi universidad que también asistieron al evento, personas que lamento no haber conocido antes. Pero la razón por la cual terminé en Jalisco fue la misma que me entristeció las cosas. Lo que creí era una oportunidad de mejorar mi relación me hizo darme cuenta en realidad de que tan mal estaban ya las cosas.

Circuito de muestreo y retención

Este circuito puede encontrarse en la página 706 del libro Circuitos Electrónicos Discretos e Integrados de Donald L. Schilling. Es un circuito inversor de muestreo y retención que utiliza un FET de canal p como dispositivo de conmutación. El diodo D1 hace que la tensión en el drenaje del FET se mantenga fijada en 0.7 V haciendo que el voltaje Vsg nunca exceda -4.3 V independientemente del valor de la señal de entrada V1. Si la señal V1 se vuelve negativa, las funciones de las terminales drenaje y fuente se invierten, permitiendo que el circuito se comporte de manera similar a un interruptor ideal. La simulación de la respuesta del circuito es la siguiente:

Buscando a Waldo con Matlab

Una aplicación entretenida de la correlación cruzada normalizada es la detección de una imagen patrón en una imagen de mayor tamaño. Esta correlación está definida matemáticamente como 

dónde f(x,y) representa a la función de imagen y t(x,y) la función de templete o imagen patrón que se desea detectar. En nuestro programa ese templete será este segmento de imagen dónde aparece Waldo:

Nuestra función principal será el siguiente mapa en el que habrá que encontrar a Waldo:

Para encontrarlo utilizaremos la función normxcorr2(). Esta función retornará un arreglo bidimensional resultado de la correlación cruzada del templete y la imagen. Para encontrar la posposición de Waldo en la imagen bastará con encontrar el punto donde la función alcanza su máximo. El arreglo resultante será tan grande como la imagen del mapa por lo que habrá que seleccionar una pequeña región alrededor del pico para poder visualizarlo mejor:

 Para encontrar la posición del pico utilizamos la función max() con la siguiente sintaxis:

[pico,indice] = max(c(:)); % Obtener valor del pico y su índice

El arreglo c representa a la función de de correlación. Hasta aquí la variable pico contiene el valor del máximo y la variable indice contiene la posición del valor máximo como si la matriz c estuviera distribuida en un arreglo vectorial. Para conocer la verdadera poción del pico en la imagen se necesita la función  ind2sub():

[y,x] = ind2sub(size(c),indice); % Obtener posición en la imagen 

Teniendo ahora la posición de Waldo solo queda mostrar la imagen completa con un rectángulo superpuesto para señalarlo:

 El programa completo es quizá más compacto de lo que pudieron haber pensado

clc,clear
mapa = imread('Waldo.jpg'); %Carga imagen del mapa
waldokernel = imread('waldok.jpg'); % carga templete de Waldo
c = normxcorr2(waldokernel(:,:,1),mapa(:,:,1)); % Correlación cruzada normalizada
[pico,indice] = max(c(:)); % Obtener valor del pico y su índice
[y,x] = ind2sub(size(c),indice); % Obtener posición en la imagen
ccut = c(y-45:y+45,x-45:x+45); % Recortar región alrededor del pico
imshow(mapa)
hold on
rectangle('Position',[x-50,y-43,70,70], 'LineWidth',2)
figure(2),surf(ccut), shading flat, title('Pico en Correlación Cruzada')

Elisyum

En un conversación divagada le comenté a un amigo una idea que he traído en la cabeza desde hace mucho. Se trata de construir una ciudad desde cero con todo lo mejor que México puede ofrecer: las mejores universidades, centros de investigación, hospitales y fabricas de alta tecnología así como las oficinas de las empresas más grandes, es decir, una Hong Kong mexicana en la cosa de Veracruz o Oaxaca. Me hizo ver inmediatamente que esa idea le recordó a la película de Elisyum. Quizá tenga razón. Aumentar aún más la desigualidad en el país dista de ser una solución. Pero me queda la curiosidad. ¿Qué pasaría si existiera una ciudad así?

Problema al implementar un programa asíncrono en VHDL

Supongamos que tenemos un programa muy simple en VHDL en el que prendemos y apagamos dos leds mediante dos interruptores: 

library ieee;
use ieee.std_logic_1164.all;

entity leds is
port( a,b : in std_logic;
     s1,s2: out std_logic);   
end leds;

architecture control of leds is
begin

s1 <= a;
s2 <= b;

end control;

Para la tarjeta de desarrollo Basys2 nuestro archivo .ucf quedaría:

# Interruptores
NET "a" LOC = P11;
NET "b" LOC = L3;

# Leds
NET "s1" LOC = M5;
NET "s2" LOC = M11;

Hasta aquí todo parece en orden e incluso nuestro programa funciona bien en la simulación. Pero un problema muy común entre los estudiantes de los primeros cursos de sistemas digitales es que al momento de cargar el archivo .bit de un programa asíncrono como este a una tarjeta de desarrollo, ésta se queda sin hacer nada. Esto ocurre porque la tarjeta espera arrancar por default con el oscilador interno aunque no lo usemos en el programa (razón por la que este problema muy rara vez se presenta en programas que si lo usan). Este problema se resuelve simplemente haciendo click derecho sobre "Generate Program File", buscar "Process Properties" que nos abrirá la siguiente ventana en la debemos buscar la categoría "Startup Options" y cambiar la opción de FPGA Start-Up Clock de CCLK a JTAG Clock:

Control PID para el modelo simple de una masa móvil

Supongamos que tenemos un pequeño vehículo de masa 'm' que se encuentra en una posición inicial x0 que queremos llevar hasta una posición final xr. Para simplificar las cosas supondremos que no existe fricción entre las ruedas y el suelo ni resistencia al aire. El modelo de nuestra planta queda descrito entonces por la 2da Ley de Newton:

dónde la fuerza F(t) es la entrada y la posición x(t) nuestra salida de la planta. Obteniendo la transformada de Laplace,su función de transferencia nos queda:

Observe que cuando a 'm' se le asigna una masa unitaria G(s) se convierte en un doble integrador. Para este modelo, como debe haberse tratado en cualquier curso de control, un controlador proporcional resulta ineficaz. Un controlador de este tipo únicamente mantendría oscilando el carrito al rededor de la posición deseada sin alcanzar nunca la estabilidad. Incluso considerando la resistencia al aire, este tipo de controlador mostrará una respuesta transitoria indeseable. Para control ideal, donde el carrito acelere y desacelere suavemente hasta detenerse justo (casi en este caso sin fricción ni resistencia al aire) en la posición que queremos requerimos un controlador PID. Las ganancias para controlar un doble integrador ideal son:

Corriendo nuestro modelo en Simulink estos son son los resultados:

 

Pruebas con adaptador Canon para telescopio (impreso 3D)

Hace poco mandé a imprimir en la Inventoteca una montura EF que se puede descargar en Thingiverse. Después de un intento fallido y varias vueltas, finalmente mi novia y yo lo probamos en su telescopio y funcionó de maravilla. ¡He aquí algunas fotos!:

 I

I miss you and every single star is a memory. Then I ask myself, what's all this starfield above me? I may say it's almost everything; matter, vastness... even an endless collection of frames of you.

II

Anoche soñé que te escribía un poema infinito. Te decía que estaba escrito en una sola hoja de papel. Pienso, a modo de analogía, en el sediento que sueña con el agua que nunca lo calma. Yo, en cambio, te escribo en líneas que forman copos de nieve; fractales de Koch.

Chapultepec