Supongamos que tenemos un pequeño vehículo de masa 'm' que se encuentra en una posición inicial x0 que queremos llevar hasta una posición final xr. Para simplificar las cosas supondremos que no existe fricción entre las ruedas y el suelo ni resistencia al aire. El modelo de nuestra planta queda descrito entonces por la 2da Ley de Newton:
dónde la fuerza F(t) es la entrada y la posición x(t) nuestra salida de la planta. Obteniendo la transformada de Laplace,su función de transferencia nos queda:
Observe que cuando a 'm' se le asigna una masa unitaria G(s) se convierte en un doble integrador. Para este modelo, como debe haberse tratado en cualquier curso de control, un controlador proporcional resulta ineficaz. Un controlador de este tipo únicamente mantendría oscilando el carrito al rededor de la posición deseada sin alcanzar nunca la estabilidad. Incluso considerando la resistencia al aire, este tipo de controlador mostrará una respuesta transitoria indeseable. Para control ideal, donde el carrito acelere y desacelere suavemente hasta detenerse justo (casi en este caso sin fricción ni resistencia al aire) en la posición que queremos requerimos un controlador PID. Las ganancias para controlar un doble integrador ideal son:
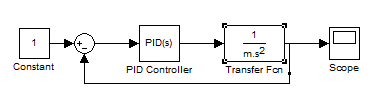
Corriendo nuestro modelo en Simulink estos son son los resultados:



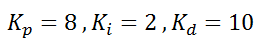

No hay comentarios:
Publicar un comentario