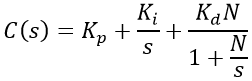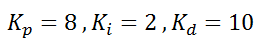Toolbox de Control para Python

Para aquellos que busquen un sustituto de código abierto para Matlab hay una buena noticia: Existe el módulo Python Control Systems Library. Acabo de probarlo y me parece mucho mejor que otras alternativas como los toolbox de control para Scilab y Octave. Si usan Anaconda, pueden instalarlo desde la terminal usando conda:

$ conda install -c conda-forge control

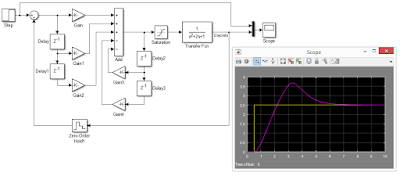
Quiero mostrarles algunos ejemplos simples utilizando el modelo de un motor NXT de Lego que describo en una entrada anterior. El modelo es el siguiente:

Creamos el objeto del modelo de la siguiente forma:

#Modelo como función de transferencia
num = [193.3]
den = [1.0, 18.735, 0.0]
sys = ctrl.tf(num,den) #Lazo abierto
print(sys)

El print nos mostrara la función de transferencia como una fracción en texto (al igual que en Matlab). Vamos a graficar ahora la respuesta al escalón de la planta en lazo cerrado:

#Modelo en lazo cerrado
sys_cl = ctrl.feedback(sys,1)

#Respuesta al escalón
t,y = ctrl.step_response(sys_cl)

#Graficas
plt.plot(t,y)
plt.grid(True)
plt.title(u"Respuesta al escalón")
plt.xlabel("segundos")

Lo que nos dará el siguiente resultado:

Para obtener el diagrama de bode:

plt.figure(2)
ctrl.bode_plot(sys)

Para visualizar el diagrama de polos y zeros:

from control.pzmap import pzmap 

plt.figure(3)
polos,zeros = pzmap(sys_cl), plt.grid(True)
print(polos[0])
print(polos[1])

¡Trataré de crear notebook's con más ejemplos y subirlos en mi GitHub!

Identificación de la función de transferencia de un motor de Lego Mindstorms NXT

Utilizando la App de System Identification Toolbox de Matlab es muy sencillo estimar experimentalmente la función de transferencia de un sistema dinámico. Básicamente, existen 3 formas de identificar la planta de un sistema dinámico: el modelo de caja negra, el modelo de caja blanca y el modelo de caja gris. En el modelo de caja blanca se obtiene la función de transferencia a partir de los principios físicos conocidos sobre el sistema (que es lo que suele hacerse en un primer curso de sistemas de control al obtener la planta de un sistema masa-resorte-amortiguador). Sin embargo, cuando se trata de sistemas reales esto o suele ser muy complicado. El método de modelado por caja negra se encarga de estimar la función de transferencia con herramientas estadísticas utilizando únicamente una función de entrada de prueba y la función de respuesta de la planta ante dicha función:

Para la que la identificación sea certera es un requisito que u(t) tengo un ancho de banda muy amplio. Esto le permite al algoritmo de estimación tener más información disponible para la estimación del modelo. Idealmente la función que cumple con ancho de banda infinito es la delta de Dirac, sin embargo, al ser imposible de generar físicamente se opta en la practica por usar secuencias pseudoaleatorias binarias (PRBS's). Estas secuencias pueden generarse con un registro de corrimiento de retroalimentación lineal (LFSR) y tienen características espectrales de ruido blanco lo que las hace ideales para ser usadas como señales de prueba. La descripción de los generadores de PRBS's es todo un tema aparte del que espero escribir a detalle más adelante, pero pueden darse muy buena idea de como funcinan con este documento.

Para esta práctica se requiere tener instalar el paquete de soporte de  Lego Mindstorms para Simulink. Pueden instalarlo ejecutando el comando supportPackageInstaller en la ventana de comandos de Matlab y buscando Lego Mindstorms NXT. El modelo implementado en el NXT es el siguiente:

 








Este diagrama nos permite adquirir los datos tanto de la función de entrada como la de salida y los envía al workspace. Para poder hacer la adquisición a la PC debe ejecutarse en modo external. [Aquí pueden ver un video tutorial para hacer esto]. Los datos obtenidos son los siguentes:

Estas dos señales son las que utilizaremos en al app para realizar la identificación. Esta aplicación tiene una interfaz gráfica muy sencilla de utilizar.[Aquí hay un videotutorial en español para aprender a usarla]. Después de experimentar con varias combinaciones de polos y ceros, el modelo preliminar que logró un acierto del 96.12 % fue el siguiente:

Este aún es el modelo crudo encontrado por el identificador y es necesario ajustarlo. Lo primero que salta a la vista el el termino 5,434e-11 que es despreciable y eliminaremos en el modelo final. Lo que resta es hacer un ajuste de ganancia. Para ello requerimos la respuesta experimental en lazo cerrado del motor ante un escalón unitario. Ejecutamos entonces el siguiente diagrama a bloques para poder obtenerlo:

Teniendo los datos de la respuesta experimental, debemos ahora compararlo con la respuesta teórica de nuestro modelo ajustando la ganancia hasta observar resultados favorables (debe haber algún procedimiento analítico para esto, pero lo he realizado de forma empírica). El diagrama del modelo teórico, junto con el modelo de caja blanca realizado por la Universidad  Politécnica de Madrid[1] como segunda referencia, es el siguiente:

 Las respuestas fueron las siguientes:

   Con esto queda verificado que la función de transferencia final de posición angular (en grados) contra potencia (%) nos queda:

 La ventaja de este proceso es que puede repetirse para caracterizar la función de transferencia de los motores con carga como puede ser un brazo robótico o un robot móvil, algo que representaría un proceso tedioso con el enfoque de caja blanca. Adelantantome a la petición de los archivos:

Descargar Modelos

Modelo lineal de un motor DC

El modelo lineal de un motor eléctrico de DC consiste en 2 ecuaciones diferenciales acopladas: el modelo eléctrico y el modelo mecánico. Debido a que ambos modelos están relacionados podemos escribir un modelo general el cual nos permitirá obtener una función de transferencia. En este ejemplo encontraremos la función de transferencia que relacione voltaje (entrada) con posición angular (salida). Primero, observemos el diagrama del circuito equivalente de la armadura del motor y el diagrama de cuerpo libre de rotor:

Para obtener la ecuación diferencial para el modelo eléctrico consideramos la ley de voltajes de Kirchoff:

 La fuerza contra-electromotriz se genera al iniciar el movimiento del rotor debido a que el campo magnético fijo del estator induce un voltaje en el devanado de la armadura (este voltaje es negativo con respecto al voltaje de entrada). La fcem es proporcional a la velocidad angular del rotor por lo que la constante Kb puede determinarse experimentalmente graficando el voltaje en las terminales del motor contra la velocidad angular del rotor (se verá que la relación no es realmente lineal en un intervalo grande pero puede usarse sólo la región lineal como una aproximación para el modelo).

Para obtener el modelo mecánico consideramos la segunda ley de Newton para movimiento angular:

Dónde J y b son el momento de inercia del rotor y el coeficiente de amortiguamiento por fricción respectivamente. Vemos que el torque es proporcional a la corriente en el motor. Asumiendo que no hay perdidas electromagnéticas, por fricción ni por calor, la potencia mecánica en el rotor debe igualar a la potencia eléctrica de manera que :

Por lo que el valor para el factor de fcem encontrado experimentalmente puede ser usado como valor para Kt. Observamos ahora que las ecuaciones (1) y (2) están relacionadas por la función de corriente.Para facilitar la sustitución obtendremos primero la transformada de Laplace de ambas ecuaciones:

Despejando I(s) de (4) y sustituyendo en (3) obtendremos el modelo unificado para el motor DC. Teniendo ya una sola ecuación obtenemos la función de transferencia posición/voltaje:

Ejecutando el siguiente código en Matlab asignando algunos valores a las constantes obtenemos su respuesta al escalón unitario en lazo cerrado:

J = 3.2284E-6;
b = 3.5077E-6;
K = 0.0274;
R = 4;
L = 2.75E-6;
s = tf('s');
P_motor = K/(s*((J*s+b)*(L*s+R)+K^2))
sys_cl = feedback(P_motor,1)
step(sys_cl)

Nota: Esto es lo que se conoce como identificación de sistema de caja blanca. Si no conocen ningún parámetro físico del motor, pueden usar el procedimiento de identificación de caja negra que describo aquí.

Referencias:
DC Motor Position: System Modeling, University of Michigan
DC Motor, MathWorks
DC Motor, How It Works? [video subtitulado en español], Learn Engineering

Implementación de un controlador PID discreto en un PIC18F2550

En esta entrada se utilizará el método desarrollado en la entrada anterior, por lo que saltarán algunos pasos durante el proceso. En esa entrada se implementó un controlador PID para una planta descrita por un doble integrador. En esta ocasión haremos una simulación de un controlador PID implementado en un PIC para controlar una planta construida con amplificadores operacionales. Si bien es posible construir un doble integrador físicamente, resulta impráctico debido a la saturación provocada por la acumulación continua. Para resolver esto, esta planta estará caracterizada por dos integradores con reset resistivo o integradores de ganancia controlada (que una forma elegante de llamar a un filtro pasa-bajas activo de un solo polo) [1].  Eligiendo los valores de resistencia y capacitancia de tal manera que cada integrador tenga ganancia unitaria, la función de transferencia de los 2 integradores nos queda:

 Para controlar esta planta utilizaremos el siguiente controlador discreto a partir de la transformación backward Euler:

Dónde:

Obteniendo transformada inversa, la salida de control descrita como ecuación de diferencias nos queda:

Hacemos la siguiente sustitución de coeficientes:

Estos coeficientes pueden encontrarse manualmente siguiendo el procedimiento descrito aquí, o ejecutando éste programa de Matlab: [PID_Proteus.m]. Teniendo estos valores podemos realizar una verificación de la ecuación en Simulink:

Algo muy importante que se debe notar es que en esta simulación se está considerando la limitación física de la saturación de la salida del controlador real. Sin esta limitación la respuesta del controlador sería más rápida y con un sobreimpulso mucho menor. Sabiendo ahora que nuestra ecuación de diferencias es correcta podemos proceder a escribir el programa en el PIC en lenguaje C con el compilador MikroC. El programa completo se adjuntará más adelante. La función de control principal queda descrita como:

void pid(void) // Función para el controlador
{
   e2=e1; e1=e0; u2=u1; u1=u0; // update de variables
   y = ADC_Read(0);   // Lectura analógica por AN0
   yd = (double) y;  // Conversión a double
   vin = (yd/1023*5);
   y = ADC_Read(1);   // Lectura analógica por AN1
   yd = (double) y;  // Conversión a double
   reff = (yd/1023*5);
   e0 = reff - vin;  // Error
   u0 = ke0*e0 + ke1*e1 + ke2*e2 - ku1*u1 - ku2*u2; // Ecuación de diferencias
   salida = (int) floor(((u0+5)/10)*1023);
   if (salida > 1023) salida = 1023;  // Saturación de DAC
   if (salida <= 0) salida = 0;
   DAC_Output(salida); // Enviar dato
}

Es muy importante que ésta función sea ejecutada dentro de una rutina de interrupción de manera que se tenga control del tiempo de muestreo Ts en exactamente 0.01 segundos para que el controlador funcione correctamente. Para la salida analógica del controlador se esta utilizando un DAC LTC1660 [2][3]. Compilando el programa y simulando en Proteus:

 Nota: El relay en la simulación lo único que hace es evitar que la salida bipolar del DAC envíe un voltaje de saturación negativo al inicio [ver este programa].

Descargar archivos

Implementación de un controlador PID discreto

Supongamos que queremos controlar el mismo modelo de una masa móvil sin fricción que habíamos tratado en esta entrada cuya función de transferencia es la siguiente:

Dados las ganancias del controlador PID que se habían considerado (recomiendo utilizar el app PID Tuning de Matlab si no tienes estos valores para la planta de tu interés) :

La función de transferencia en tiempo continuo de nuestro controlador nos queda:

En la práctica es recomendable utilizar un LPF en la etapa derivativa a modo de reducir el ruido. En este caso la FT es:

Dónde N representa la frecuencia de corte del filtro que suele ser de 100 radianes/s. Teniendo la función de transferencia de nuestro controlador, el proceso de implementación de este controlador en un sistema digital (PIC, Arduino, FPGA, etc) es el siguiente:

La ecuación de diferencias es la que describirá el algoritmo que deberemos implementar en algún lenguaje de programación o un lenguaje de descripción de hardware. Para realizar la transformación entre la FT en dominio de Laplace al dominio de Z debemos considerar las siguientes aproximaciones numéricas para la derivada:

De aquí es fácil notar que podemos representar a la variable s en terminos de z (dónde Ts es el periodo de muestreo) de las siguientes maneras:

Estas 2 transformaciones de la variable s tienen propiedades distintas. Mientras la transformación backward Euler es estable siempre que la FT en tiempo continuo sea estable, la transformación forward Euler no lo es en todos los casos. (Para más detalles consultar la sección 19.2.3.1 de "Pasive, Active and Digital Filters", Wai-Kai Chen [1]). Para este ejemplo utilizaremos la transformación forward Euler, por lo que nuestro controlador queda representado en tiempo discreto por la TF:

Para este ejemplo se sabe de antemano que este controlador es estable pero si se arriesga a utilizar foward Euler se recomienda verificar estabilidad (puede usarse sisotool de Matlab).  Verificamos en Simulink que nuestro controlador funcione correctamente:

Ahora podemos proceder a la conversión de formatos de la FT. Para eso utilizamos el este programa de Matlab: PIDdiscreto.mat. Usando los datos que nos muestra el programa la FT nos queda:

Reordenando (click para agrandar):

Calculando transformada inversa:

Finalmente, verificamos que la ecuación de diferencias sea correcta en Simulink:

En una próxima entrada se implementará este controlador en un código en C para PIC y Arduino.

Control PID para el modelo simple de una masa móvil

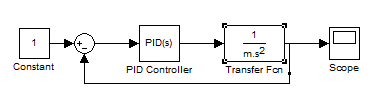
Supongamos que tenemos un pequeño vehículo de masa 'm' que se encuentra en una posición inicial x0 que queremos llevar hasta una posición final xr. Para simplificar las cosas supondremos que no existe fricción entre las ruedas y el suelo ni resistencia al aire. El modelo de nuestra planta queda descrito entonces por la 2da Ley de Newton:

dónde la fuerza F(t) es la entrada y la posición x(t) nuestra salida de la planta. Obteniendo la transformada de Laplace,su función de transferencia nos queda:

Observe que cuando a 'm' se le asigna una masa unitaria G(s) se convierte en un doble integrador. Para este modelo, como debe haberse tratado en cualquier curso de control, un controlador proporcional resulta ineficaz. Un controlador de este tipo únicamente mantendría oscilando el carrito al rededor de la posición deseada sin alcanzar nunca la estabilidad. Incluso considerando la resistencia al aire, este tipo de controlador mostrará una respuesta transitoria indeseable. Para control ideal, donde el carrito acelere y desacelere suavemente hasta detenerse justo (casi en este caso sin fricción ni resistencia al aire) en la posición que queremos requerimos un controlador PID. Las ganancias para controlar un doble integrador ideal son:

Corriendo nuestro modelo en Simulink estos son son los resultados:

 

Cuadricópteros

Tremendas maniobras en el aire. Soy retebien pinche fan de los robots voladores. Un aplauso a la Universidad de Pensylvania, por favor. No dejen de ver éste donde elevan pequeñas cargas de forma coordinada.

BotJunkie