Dados las ganancias del controlador PID que se habían considerado (recomiendo utilizar el app PID Tuning de Matlab si no tienes estos valores para la planta de tu interés) :
La función de transferencia en tiempo continuo de nuestro controlador nos queda:
De aquí es fácil notar que podemos representar a la variable s en terminos de z (dónde Ts es el periodo de muestreo) de las siguientes maneras:
Estas 2 transformaciones de la variable s tienen propiedades distintas. Mientras la transformación backward Euler es estable siempre que la FT en tiempo continuo sea estable, la transformación forward Euler no lo es en todos los casos. (Para más detalles consultar la sección 19.2.3.1 de "Pasive, Active and Digital Filters", Wai-Kai Chen [1]). Para este ejemplo utilizaremos la transformación forward Euler, por lo que nuestro controlador queda representado en tiempo discreto por la TF:
Para este ejemplo se sabe de antemano que este controlador es estable pero si se arriesga a utilizar foward Euler se recomienda verificar estabilidad (puede usarse sisotool de Matlab). Verificamos en Simulink que nuestro controlador funcione correctamente:
Ahora podemos proceder a la conversión de formatos de la FT. Para eso utilizamos el este programa de Matlab: PIDdiscreto.mat. Usando los datos que nos muestra el programa la FT nos queda:
Calculando transformada inversa:
Finalmente, verificamos que la ecuación de diferencias sea correcta en Simulink:
En una próxima entrada se implementará este controlador en un código en C para PIC y Arduino.



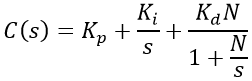







2 comentarios:
Está bueno tu aporte amigo, pero tienes algunos errores en tus enunciados, especialmente en el filtro low-pass que colocaste en la función de transferencia del PD el cual es
Kd* N
----------
1 + N(1/s)
Me funcionó tu esquema, gracias!
Tenías razón. Ya hice las correcciones de las ecuaciones, gracias!
Publicar un comentario